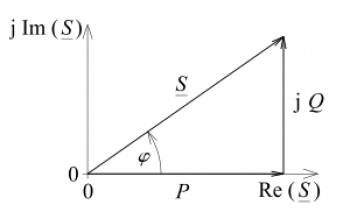
El triangle de potències, també conegut com a triangle de Watt, és una representació gràfica utilitzada en la teoria de l'electricitat per analitzar la distribució de potència en un circuit de corrent altern (CA).
Es basa en les propietats trigonomètriques d'un triangle rectangle, cosa que permet calcular i comprendre la relació entre les tres potències fonamentals d'un sistema elèctric:
- Potència aparent (\( S \)) : Representa la potència total subministrada al circuit i es mesura en voltiampers (VA). És la combinació vectorial de la potència activa i la reactiva.
- Potència activa (\( P \)) : És la potència útil que es transforma en treball real, com la il·luminació o el moviment de motors. Es mesura en watts (W).
- Potència reactiva (\( Q \)) : És la potència que no realitza treball útil però és necessària per al funcionament d'equips amb elements inductius (com a transformadors i motors). Es mesura en voltampers reactius (VAR).
Fórmula del triangle de potències
El triangle està compost per tres costats, on:
- La hipotenusa representa la potència aparent (\( S \)).
- El catet adjacent és la potència activa (\( P \)), relacionada amb el cosinus de l'angle de fase (\( \cos\theta \)).
- El catet oposat és la potència reactiva (\( Q \)), relacionada amb el si de l'angle de fase (\(\sense\theta \)).
- Matemàticament, la relació entre aquestes potències s'expressa mitjançant el teorema de Pitàgores:
\[ S^2 = P^2 + Q^2 \]
El factor de potència (FP) es defineix com la relació entre la potència activa i la potència aparent:
\[ FP = \cos\theta = \frac{P}{S} \]
Quan el factor de potència és baix, significa que hi ha una alta proporció de potència reactiva, cosa que redueix l'eficiència del sistema elèctric.
Exemples pràctics del triangle de potències
A continuació mostrem tres exemples pràctics
Motor elèctric amb factor de potència baix
Un motor d'inducció consumeix 10 kW de potència activa i té una potència reactiva de 6 kVAR a causa de la naturalesa inductiva.
La potència aparent serà:
\[ S = \sqrt{(10^2 + 6^2)} = \sqrt{100 + 36} = \sqrt{136} \aprox. 11,66 \text{ kVA} \]
Sistema d'il·luminació amb correcció de factor de potència
Un conjunt de làmpades LED consumeix 5 kW amb una potència reactiva de 1 kVAR.
La potència aparent serà:
\[ S = \sqrt{(5^2 + 1^2)} = \sqrt{25 + 1} = \sqrt{26} \aprox. 5,1 \text{ kVA} \]
Transformador amb càrrega inductiva
Un transformador subministra 50 kW a un sistema amb una càrrega inductiva que requereixi 30 kVAR.
La potència aparent del sistema serà:
\[ S = \sqrt{(50^2 + 30^2)} = \sqrt{2500 + 900} = \sqrt{3400} \aprox. 58,3 \text{ kVA} \]
Per què serveix el triangle de potències?
El triangle de potències és una eina fonamental en l'anàlisi i el disseny de sistemes elèctrics. Les seves aplicacions inclouen:
Càlcul de la potència elèctrica
Permet determinar la distribució de potència en un circuit:
- La potència aparent (S) total subministrada.
- La potència activa (P), que es converteix en energia útil.
- La potència reactiva (Q), que representa lenergia intercanviada entre components inductius i capacitius.
Optimització del rendiment del circuit
En conèixer la distribució de potències, es poden minimitzar les pèrdues energètiques i millorar el factor de potència, cosa que redueix el consum innecessari d'energia reactiva i optimitza l'ús de la xarxa elèctrica.
Disseny de sistemes elèctrics
S'usa per al dimensionament d'equips elèctrics, assegurant que els transformadors, generadors i cables siguin adequats per manejar la potència requerida sense sobrecàrrega ni pèrdues excessives.
Correcció del factor de potència
Molts sistemes elèctrics industrials requereixen bancs de condensadors per compensar la potència reactiva i millorar el factor de potència, reduint així la demanda denergia de la xarxa i disminuint costos operatius.
Anàlisi de falles i manteniment preventiu
El triangle de potències permet detectar problemes en sistemes elèctrics, com pèrdues denergia degudes a alta reactància o desajustos en la càrrega, ajudant a prevenir falles i optimitzar el manteniment.
Exercici resolt sobre el triangle de potències
Declaració:
Hi ha un circuit elèctric amb una potència aparent de 800 VA i un factor de potència de 0,8. Calcular la potència activa i la potència reactiva del circuit.
Solució:
Primer podem calcular la potència activa (P) del circuit utilitzant la fórmula P = S x cos(θ), on θ és l'angle de fase entre el corrent i el voltatge. En aquest cas, com que el factor de potència (FP) és igual a 0,8, sabem que cos(θ) = FP = 0,8. Per tant, podem calcular la potència activa com segueix:
\[
P = 800 \, VA \times 0,8 = 640 \, W
\]
La potència activa del circuit és de 640 watts.
Després, podem calcular la potència reactiva (Q) del circuit utilitzant la fórmula Q = S x sin(θ). Sabem que l'angle de fase (θ) es pot calcular a partir del factor de potència utilitzant la fórmula següent:
\[
\cos(\theta) = \text{FP} \quad \Rightarrow \quad \sin(\theta) = \sqrt{1 - \cos^2(\theta)}
\]
En aquest cas, com a FP = 0,8, podem calcular sin(θ) com segueix:
\[
\sin(\theta) = \sqrt{1 - 0,8^2} = \sqrt{1 - 0,64} = \sqrt{0,36} = 0,6
\]
Per tant, podem calcular la potència reactiva de la manera següent:
\[
Q = 800 \, VA \times 0.6 = 480 \, VAR
\]
La potència reactiva del circuit és de 480 voltampers reactius.
Per tant, la potència activa del circuit és de 640 W i la potència reactiva és de 480 VAR.