El triangle, una figura geomètrica composta per tres segments que connecten tres vèrtexs diferents no alineats, representa una de les formes poligonals fonamentals a la geometria. La seva rellevància en la ciència i la tecnologia es remunta a temps antics, atès que és una de les figures geomètriques més essencials i àmpliament emprades.
Un tret significatiu dels triangles és la seva invariabilitat, cosa que els converteix en elements crucials en el disseny arquitectònic, com la Torre Eiffel, basada en una composició de formes triangulars, i l'enginyeria, incloent-hi estructures fixes per a panells solars. A més, tenen un paper fonamental en la geometria, ja que tots els polígons es poden descompondre en triangles.
Característiques dels triangles
Els triangles són figures geomètriques fonamentals amb diverses característiques que en defineixen l'estructura i les propietats. Aquí hi ha algunes de les característiques més importants dels triangles:
- Tres costats Els triangles són polígons que tenen exactament tres costats. Aquests costats són segments de línia que connecten tres punts anomenats vèrtexs.
- Tres angles : Cada triangle consta de tres angles interiors als seus vèrtexs.
- Suma d'angles En un triangle, la suma dels angles interns és igual a 180 graus. Això és vàlid per a qualsevol tipus de triangle, ja sigui equilàter, isòsceles o escalè.
- costats i angles corresponents : En un triangle, els costats i angles corresponents són iguals en triangles congruents. La congruència es refereix a la igualtat de forma i mida.
- Alçada i mitjana : En un triangle, l'alçada és un segment de línia perpendicular a un costat i que passa pel vèrtex oposat. La mediana és un segment que connecta un vèrtex amb el punt mitjà del costat oposat.
Tipus de triangles
Aquestes figures geomètriques es poden classificar seguint diferents criteris:
Per la mida dels angles interiors pot ser:
- Triangle acutangle : tots els angles interiors són aguts (menors de 90 graus).
- Triangle obtusangle : existeix un angle major de 90 graus.
- Triangle rectangle : un dels angles és de 90 graus, un angle recte. En aquest cas, els dos costats que formen un angle recte s'anomenen catets i el costat oposat a l'angle recte s'anomena hipotenusa.
Com en geometria euclidiana, la suma dels angles d'un triangle és 180º. Per tant, almenys dos angles al triangle han de ser aguts (menys de 90º)
Pel nombre de costats iguals aquestes figures poden ser:
- Triangle escalè : els tres costats no són iguals.
- Triangle isòsceles : dos costats són iguals. Aquests costats es diuen costat, el tercer costat es diu base. En un triangle isòsceles, els angles a la base són iguals.
- Triangle equilàter : els tres costats són iguals. En un triangle equilàter, tots els angles són iguals a 60°.
Calculeu l'àrea i el perímetre d'un triangle
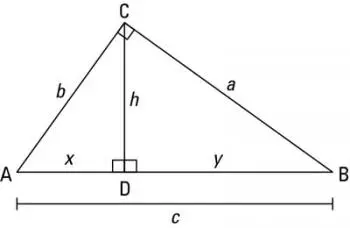
Basant-nos en la figura de la part inferior, per obtenir el perímetre i l'àrea d'un triangle, podem utilitzar les fórmules següents:
Perímetre
Per calcular el perímetre simplement hem de sumar la longitud dels costats de la figura: a + b + c.
Àrea
La fórmula per treure l'àrea d'un triangle és la meitat del producte de la base (no dels costats) per l'alçada:
A = (b · h) / 2
En cas que desconeguem l'alçada podem aplicar la fórmula d'Heron.
On:
-
a, bic correspon als tres costats de la figura geomètrica.
-
A és l'àrea
-
s és el semiperímetre (es troba el perímetre i es divideix per dos):
En cas d'un triangle rectangle, un dels catets és la base i l'altre correspon a l'alçada l'alçada. D'aquesta manera, resulta més senzill calcular l'àrea.
Propietats i teoremes
Teorema de Pitàgores
El teorema de Pitàgores és un dels resultats geomètrics més famosos i útils. S'aplica a triangles rectangles, amb un angle recte (90 graus). El teorema estableix que en un triangle rectangle, el quadrat de la longitud de la hipotenusa és igual a la suma dels quadrats de les longituds dels altres dos costats. Matemàticament, s'expressa com:
a² + b² = c²
On "a" i "b" són les longituds dels catets i "c" és la longitud de la hipotenusa.
El teorema de Pitàgores és fonamental en geometria i trigonometria i s'aplica a una àmplia varietat de problemes, des de càlculs de distàncies en mapes fins a la resolució d'equacions quadràtiques.
Teorema de la Bisectriu
El teorema de la Bisectriu fa referència a la bisectriu d'un angle en un triangle. Estableix que la bisectriu d'un angle dividix el costat oposat a l'angle en dos segments que són proporcionals als altres dos costats del triangle. Matemàticament, s'expressa com:
a/d = b/e
On "a" i "b" són les longituds dels costats del triangle, i "d" i "e" són les longituds dels segments en què la bisectriu divideix el costat oposat.
Aquest teorema és útil per calcular segments a triangles i trobar punts d'intersecció en angles bisectors.
Teorema de Tales
El teorema de Tales és una eina poderosa per relacionar segments en triangles semblants. Estableix que si una línia paral·lela talla dos costats dun triangle, divideix aquests costats en segments proporcionals. Matemàticament, s'expressa com:
m/n = p/q
On "m" i "n" són les longituds dels segments a una banda del triangle, i "p" i "q" són les longituds dels segments corresponents a l'altra banda.
El teorema de Tales és fonamental en la resolució de problemes geomètrics i en la demostració de propietats de triangles semblants.