La geometria és una branca de les matemàtiques que s'enfoca a l'estudi de les formes, mides i propietats dels objectes geomètrics, com ara punts, línies, segments, polígons i cercles.
Un dels temes fonamentals en geometria, i en particular dels triangles, és lestudi dels angles i segments, i un dels teoremes més importants relacionats amb aquests conceptes és el teorema de la bisectriu.
Aquest teorema exerceix un paper crucial en la divisió d'angles i segments, i té aplicacions en diverses àrees de les matemàtiques i la física.
Definició d'angles i bisectriu
Abans de submergir-nos al teorema de la bisectriu, és important comprendre alguns conceptes clau en geometria. Un angle és la regió formada per dos raigs que comparteixen un punt en comú, anomenat vèrtex. Els angles es mesuren en graus, i un angle complet és de 360 graus. En molts casos, cal dividir un angle en dues parts iguals, i això ens porta a la noció d'una bisectriu.
Una bisectriu d'un angle és una línia, un raig o un segment que divideix l'angle en dos angles congruents, és a dir, dos angles que tenen la mateixa mesura. En altres paraules, la bisectriu talla l'angle per la meitat. En cas d'un angle de 90 graus, la bisectriu resultant tindria un angle de 45 graus a cada costat.
El teorema de la bisectriu en un triangle
El teorema de la bisectriu estableix que, en un triangle, la bisectriu dun angle divideix el costat oposat en segments proporcionals als altres dos costats. Això pot semblar una afirmació complexa, però la podem descompondre i entendre millor a través d'un exemple.
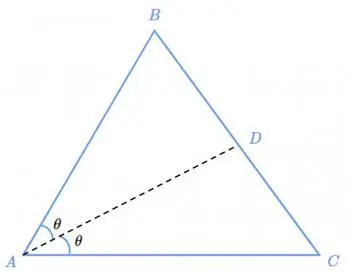
Considerem un triangle ABC, on l'angle al vèrtex A està sent bisecat per una línia que creua el costat oposat BC al punt D. El teorema ens diu que la proporció entre BD i CD és igual a la proporció entre AB i AC.
Matemàticament, això es pot expressar de la següent manera:
Aquest teorema és especialment útil en la resolució de problemes de geometria que involucren angles i segments. Podeu ajudar-nos a trobar longituds desconegudes o demostrar propietats de triangles i altres figures geomètriques.
Demostració del teorema de la bisectriu
La demostració del teorema de la bisectriu implica l'ús de propietats de triangles semblants i l'aplicació del teorema de Tales. Aquí hi ha una explicació breu de com es demostra:
-
Comencem amb el triangle ABC i la seva bisectriu que creua el costat BC al punt D.
-
Apliquem el Teorema de Tales, que estableix que si tenim dues línies paral·leles tallades per línies transversals, es creen segments proporcionals. En aquest cas, tracem una línia paral·lela als costats AC i BD que passi pel punt C.
-
Això ens dóna dos triangles semblants: ACD i ABC, on els angles són iguals i les línies són paral·leles, cosa que implica segments proporcionals.
-
Usant la propietat de semblança de triangles, podem afirmar que:
Aquesta és la igualtat que volíem demostrar, i així es completa la demostració del teorema.
Exemples d'aplicacions del teorema
El teorema de la bisectriu té diverses aplicacions en geometria i matemàtiques. Alguns dels exemples de les aplicacions més comunes inclouen:
- Resolució de problemes de geometria: El teorema es fa servir per trobar longituds desconegudes o angles en triangles i altres figures geomètriques quan es coneixen certes relacions de proporció.
- Demostració de propietats de triangles: Es fa servir per demostrar que certs triangles són semblants o que certs punts estan en una línia recta.
- Construcció geomètrica: Ajuda en la construcció d'angles biseccionats amb precisió, cosa que és útil en diverses aplicacions de disseny i arquitectura.
- Estudis de trigonometria: El teorema també s'aplica en trigonometria per resoldre problemes relacionats amb pits, cosinus i tangents.
- Resolució de problemes físics: S'utilitza físicament per comprendre les trajectòries de partícules i la direcció de les forces en sistemes físics.
