El teorema de Gauss per al camp elèctric estableix que el flux d'un camp elèctric a través d'una superfície tancada (superfície gaussiana) és donat pel quocient entre la càrrega elèctrica total dins la superfície dividit entre la constant dielèctrica absoluta del medi (ε 0 ). Qualsevol càrrega puntual externa a la superfície no contribueix de cap manera al flux total.
L'equació de Gauss forma part de les quatre equacions de Maxwell.
El camp elèctric produït per dos objectes carregats estàtics es pot obtenir per dos procediments equivalents: aplicant la llei de Coulomb o mitjançant la llei de Gauss. La llei de Coulomb és una manera més simple i directa d'expressar la força elèctrica. D'altra banda, la llei de Gauss és més subtil, més elegant i, de vegades, més útil.
El teorema de Gauss té una utilitat molt pràctica. En la seva formulació física relativa als camps elèctrics es tradueix en darrera instància en una fórmula simple, utilitzable per tots i amb implicacions pràctiques molt significatives.
El flux de càrregues que travessen la superfície gausiana és proporcional al nombre de línies de camp que la creuen.
Enunciat del teorema de Gauss
Aquí hi ha l'enunciat del teorema de Gauss per al camp elèctric: el flux d'un camp elèctric a través d'una superfície tancada està donat per la relació entre la càrrega elèctrica total dins de la superfície i la constant dielèctrica absoluta del medi.
Fórmula de la llei de Gauss
Pel que fa a la fórmula del teorema de Gauss per al camp elèctric, podem escriure
La declaració de Gauss proporciona una manera ràpida i senzilla de calcular el flux del camp elèctric a través d'una superfície tancada. Simplement es calcula la suma algebraica de totes les càrregues que estan dins de la superfície i es divideix per la constant dielèctrica absoluta.
És important destacar alguns aspectes:
-
Si pensem en el buit podem substituir la constant dielèctrica absoluta del medi ε m per la constant dielèctrica del buit el valor del qual coneixem.
-
Per calcular la suma algebraica de totes les càrregues internes, cal tenir en compte els signes de les càrregues , que poden ser càrregues positives o negatives.
-
La superfície pot tenir qualsevol forma sempre que estigui tancada.
-
El que importa és la càrrega total dins làrea de la superfície. Si hi ha altres càrregues ubicades fora de la superfície, no s'han de considerar als efectes del càlcul del cabal.
-
El teorema és vàlid per a qualsevol tipus de camp elèctric, no necessàriament uniforme a l'espai. La fórmula també és vàlida per a qualsevol configuració de càrrega.
Exemple de la llei de Gauss
Suposem que volem calcular el camp elèctric produït per una càrrega puntual i, usem la llei de Gauss per trobar-la.
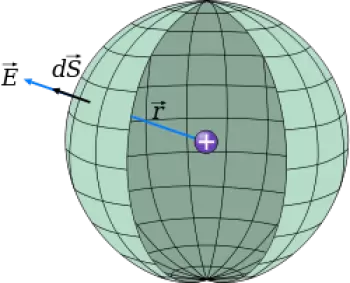
En el nostre exemple imaginem una superfície gaussiana esfèrica de radi r amb una càrrega (q) continguda al centre. Per calcular la integral de flux suposarem que, per la simetria del problema, E ha de tenir la direcció radial cap a fora de la càrrega (q). Això implica que E és paral·lel a dS a cada punt de la superfície de l'espera.
També per la simetria hem de suposar que E depèn únicament de la distància r des de la càrrega q al punt considerat, de manera que E tindrà el mateix valor per a qualsevol punt sobre l'esfera, i serà constant a la integració.
En aquestes condicions, el càlcul del flux a través de la superfície esfèrica serà:
Φ = E (4 · π · r²)
Com que la integral és simplement l'àrea de la superfície de l'esfera. Com que la càrrega total continguda dins de la nostra esfera és q, la llei de Gauss ens dóna: