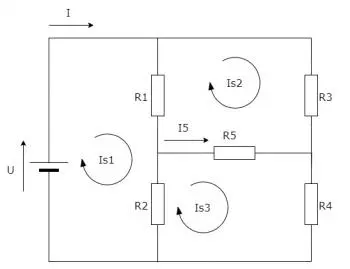
Els circuits elèctrics són una part essencial de la nostra vida moderna. Des dels dispositius electrònics més simples fins als sistemes de potència més complexos, tots depenen de la correcta comprensió i anàlisi dels circuits elèctrics.
Al segle XIX, Gustav Kirchhoff, un físic alemany, va formular les lleis que porten el seu nom i que han esdevingut els fonaments bàsics per a l'anàlisi de circuits: les lleis de Kirchhoff.
Llei de corrents de Kirchhoff (llei de nodes)
La llei de corrents de Kirchhoff, també coneguda com la llei de nodes, estableix que en qualsevol node d'un circuit elèctric, la suma algebraica dels corrents que entren i surten del node és igual a zero. En altres paraules, el corrent que flueix cap a un node és igual al corrent que surt del mateix node.
Explicació
Un node és un punt de connexió entre dos o més elements dun circuit. Com que la càrrega elèctrica no s'acumula en un node (en condicions estacionàries), la quantitat de corrent que hi entra ha d'igualar la que surt.
Matemàticament, s'expressa com:
\[ \sum I = 0 \]
O bé, igualant els corrents que entren en un node als que surten:
Si considerem un node amb diversos corrents que entren \( I_1 \),\( I_2 \),\( I_3 \) i diversos que surten \( I_4 \), \( I_5 \), on els corrents que entren es prenen com a positius i els que surten com a negatius, l'equació s'escriu així:
\[ I_1+I_2 + I_3 − I_4−I_5=0 \]
la reordenació:
\[ I_1+I_2 + I_3 = I_4 + I_5 \]
Això vol dir que la suma dels corrents que entren és igual a la suma dels corrents que surten.
Exemple de càlcul
Suposem un node amb tres corrents:
- \( I_1 = 5A \) entrant
- \( I_2 = 3A \) entrada
- \( I_3 \) és un corrent sortint però no en coneixem el valor.
Aplicant la llei de corrents podem conèixer el valor de \(I_3\):
\[ I_1 + I_2 = I_3 \]
\[ 5A+3A=I3 \]
\[ I_3=8A \]
Això indica que el corrent que surt del node és de 8 amperes.
Llei de tensions de Kirchhoff (llei de malles)
La suma algebraica de les diferències de potencial en un llaç tancat és igual a zero.
Explicació matemàtica
Un llaç és qualsevol trajectòria tancada dins un circuit. Com que l'energia elèctrica no es pot crear ni destruir dins un llaç, l'energia guanyada (per fonts de voltatge) ha de ser igual a l'energia perduda (per caigudes de tensió a resistències i altres components).
Matemàticament, s'expressa com:
\[ \sum V = 0 \]
Si en un llaç tenim una font de voltatge \( V_1 \) i diverses caigudes de tensió \( V_2 \), \( V_3 \), \( V_4 \), l'equació s'escriu així:
la reordenació:
Això significa que la suma dels voltatges subministrats per les fonts és igual a la suma de les caigudes de tensió als components del circuit.
Exemple numèric
Suposem un circuit en sèrie amb:
- Una bateria de \( V_1 = 12V \)
- Una resistència amb caiguda de tensió \( V_2 = 5V \)
- Una altra resistència amb caiguda de tensió \( V_3 = 7V \)
Aplicant la llei de tensions:
Això confirma que l'energia proporcionada per la font de 12V ha estat distribuïda entre les dues resistències.
Aplicació de les lleis de Kirchhoff
Les lleis de Kirchhoff són aplicables a qualsevol circuit elèctric, ja sigui en corrent continu (CC) o corrent altern (CA). Aquestes lleis són especialment útils per analitzar circuits complexos, on hi ha múltiples fonts de corrent i tensió, així com una varietat d'elements com a resistors, capacitors i inductors.
En aplicar les lleis de Kirchhoff, és possible establir un sistema d'equacions que es pot resoldre per determinar els corrents i les tensions en cada component del circuit. Això permet estudiar el comportament global del circuit elèctric i fer càlculs precisos per dissenyar circuits eficients i fiables.
A continuació es presenten alguns exemples d'aplicacions reals:
1. Resoldre circuits complexos
Les lleis de Kirchhoff permeten analitzar i resoldre circuits elèctrics que contenen múltiples components, fonts de corrent i tensió, i connexions complexes. En aplicar les lleis de Kirchhoff, és possible establir equacions que relacionen corrents i tensions en cada element del circuit, cosa que permet determinar-ne el comportament i calcular els valors de corrent i tensió en diferents parts del circuit.
2. Dissenyar i optimitzar circuits
En utilitzar les lleis de Kirchhoff, els enginyers elèctrics poden dissenyar i optimitzar circuits per complir els requisits específics. Aquestes lleis permeten comprendre com es distribueix el corrent i la tensió en un circuit, cosa que ajuda a identificar punts crítics, calcular la resistència necessària i assegurar un flux de corrent adequat.
3. Anàlisi de xarxes elèctriques
Les lleis de Kirchhoff també s'apliquen a l'anàlisi de xarxes elèctriques més grans, com ara sistemes de distribució d'energia o xarxes de transmissió. Aquestes lleis permeten avaluar i equilibrar el flux de corrent en diferents branques de la xarxa, identificar possibles problemes de sobrecàrrega i determinar la millor configuració per a una distribució eficient de lenergia elèctrica.
Exemples de les lleis de Kirchhoff
Aquí teniu alguns exemples que il·lustren l'aplicació de les lleis de Kirchhoff:
Exemple 1: Llei de corrents de Kirchhoff (Llei de nodes)
Suposem que tenim un circuit amb tres resistors connectats en paral·lel, alimentats per una font de corrent. Volem determinar el corrent a cada resistor.
D'acord amb la llei de corrents de Kirchhoff, la suma algebraica dels corrents que entren i surten d'un node és igual a zero. En aquest cas, el node superior es pren com a referència i el corrent total que entra a aquest node és I. Per tant, podem establir la següent equació:
On \( I_1 \), \( I_2 \) i \( I_3 \) són els corrents a cada resistor. En resoldre aquesta equació, es poden trobar els valors dels corrents a cada resistor.
Exemple 2: Llei de tensions de Kirchhoff (Llei de malles)
Suposem que tenim un circuit amb tres resistors en sèrie i una font de voltatge. Volem determinar la tensió a cada resistor.
D'acord amb la llei de tensions de Kirchhoff, la suma algebraica de les diferències de potencial (tensions) a qualsevol llaç tancat del circuit és igual a zero. En aquest cas, podem establir dues equacions utilitzant la llei de malles:
-
Per al llaç superior: \( V = V_1 + V_2 \)
-
Per al llaç inferior: \( V = -V_2 - V_3 \)
On \( V_1 \), \( V_2 \) i \( V_3 \) són les tensions a cada resistor. En resoldre aquestes equacions simultànies, podem trobar els valors de les tensions a cada resistor.
Exemple 3: Llei de tensions de Kirchhoff amb resistència
Considera un llaç amb una font de voltatge i dues resistències:
- \( V_1 = 12V \)
- \(R_1 = 4 \, \Omega \)
- \(R_2 = 2 \, \Omega \)
- \(I = 2A \)
Calculant les caigudes de tensió
Llei de tensions
\[ 12−8−4=0 \]
Es compleix la llei de tensions de Kirchhoff.