Al camp de la geometria, els plànols són uns elements bàsics i fonamentals. Definits com a superfícies infinites i planes que s'estenen en totes les direccions, els plànols són elements fonamentals que ens ajuden a comprendre les formes i estructures en dues dimensions.
En aquest article, explicarem què són els plànols en geometria, les característiques distintives i com s'apliquen en diversos contextos matemàtics i pràctics. Des del disseny de figures geomètriques fins a la resolució de problemes i el desenvolupament d'aplicacions tecnològiques, els plànols tenen un paper vital en la nostra entesa de l'espai i la forma.
Què és un pla?
En geometria, un pla és una superfície plana i infinita que s'estén a totes direccions.
Podeu pensar en un full de paper que s'estén per sempre, sense tenir gruix. En aquest cas, no hi ha límits ni vores, és com un món infinit en dues dimensions!
Característiques d'un pla
Les principals característiques que defineixen un pla a l'espai són les següents:
- Infinit en totes les adreces: Una de les característiques més importants és que s'estén infinitament en qualsevol direcció. Això vol dir que no importa com t'allunyis d'un punt al pla, sempre hi haurà més espai.
- Sense gruix: A diferència dels objectes tridimensionals, com una pilota o un cub, un pla no té gruix. Imagina't que estàs mirant un dibuix en un full de paper. El dibuix és al pla del paper, però el paper és tan prim que podem considerar que no té gruix.
- Representat per línies: En geometria, representem els plànols usant línies. Aquestes línies poden ser rectes o corbes i s'estenen a totes les direccions dins del pla. Quan dibuixem figures geomètriques en un pla, fem servir aquestes línies per mostrar com es relacionen entre si.
- Independent del sistema de coordenades: Un pla és independent del sistema de coordenades utilitzat per representar-lo. Això significa que, independentment de com es triin els eixos xey, les propietats bàsiques del pla, com la seva infinitud i la seva manca de gruix, romanen inalterades.
- Conté punts infinits: Atès que s'estén infinitament, conté infinits punts. Cada punt en el pla és únic i pot ser identificat per les coordenades, si s'utilitza un sistema de coordenades.
- No determina cap direcció preferencial: A diferència de les línies i segments, que tenen una direcció específica, el pla en si mateix no en té cap de preferencial. Així doncs, pot considerar-se com una superfície sense orientació en què les direccions són igualment vàlides.
Tipus de plans
En geometria, hi ha diversos tipus de plans que s'utilitzen per a diferents propòsits i aplicacions. A continuació, es descriuen alguns dels tipus més habituals:
- Horitzontal: Un pla horitzontal és aquell que s'estén horitzontalment en relació amb la superfície terrestre. En un sistema de coordenades tridimensional, un pla horitzontal no s'inclina ni es desvia verticalment.
- Vertical: Contrari a l'anterior, un pla vertical s'estén verticalment i és perpendicular a la superfície terrestre. El vertical és útil en geometria per representar relacions espacials a l'espai tridimensional.
- Inclinat: Un pla inclinat és aquell que no és ni horitzontal ni vertical, sinó que forma un angle respecte a tots dos. Els inclinats són comuns en problemes de física i mecànica, on s'utilitzen per estudiar forces, arracades i moviment.
- Cartesià: aquest tipus és un sistema de coordenades bidimensionals que consisteix en dos eixos perpendiculars, generalment etiquetats com a x i y. S'utilitza àmpliament en matemàtiques per representar punts, gràfics i funcions.
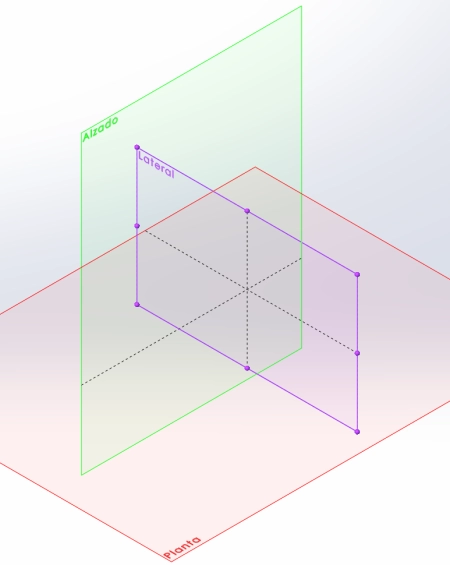
- Projecció: En dibuix tècnic i disseny, un pla de projecció es fa servir per representar objectes tridimensionals en dues dimensions. Els plànols de projecció inclouen tres plans: planta, alçat i lateral, que mostren diferents vistes de lobjecte des de diferents angles.
- Tangent: Un pla tangent és aquell que toca una superfície en un sol punt i és perpendicular a la línia que passa per aquest punt. Els plans tangents són importants en càlcul i geometria diferencial per representar la relació entre corbes i superfícies en un punt determinat.
- Paral·lel: Un pla paral·lel és aquell que no es creua amb un altre pla determinat i manté la mateixa distància en tota la seva extensió. Els plans paral·lels s'utilitzen per estudiar propietats de línies i angles en relació amb superfícies paral·leles.
- Perpendicular: Un plan perpendicular es un tipus especial que forma un àngule recte (de 90 grados) en relació a un altre pla o linea.
Diferència entre plànol i àrea
En geometria, el terme pla es refereix a una superfície bidimensional que s'estén infinitament en totes direccions, com un full de paper. És una entitat abstracta sense gruix, definida per la intersecció de dues línies o per successions de punts a l'espai.
D'altra banda, l'àrea és una mesura quantitativa de l'extensió d'una superfície bidimensional. Representa la quantitat d'espai cobert per una figura al pla i s'expressa en unitats quadrades (com metres quadrats o centímetres quadrats).
Mentre que un pla és la superfície en si mateixa, làrea és la mesura numèrica de quant espai ocupa aquesta superfície.