
S'anomena entropia a la magnitud que indica l'energia que no pot fer un treball útil en un procés termodinàmic. En general, l'univers tendeix al desordre. En conseqüència, l'entropia, és a dir, a l'augment de l'entropia, per tant, la variació positiva d'aquesta magnitud indica el sentit natural en què passa qualsevol esdeveniment en un sistema aïllat.
L'entropia (S) és una magnitud termodinàmica definida originalment com a criteri per predir l'evolució dels sistemes termodinàmics. En tot procés irreversible, el desordre del sistema augmenta i, per tant, l'entropia augmenta. Si el procés és reversible, la variació d'entropia és nul·la.
L'entropia d'un sistema és funció d'estat de caràcter extensiu. El valor d‟aquesta magnitud física, en un sistema aïllat, creix en el transcurs d‟un procés que es dóna de forma natural. El concepte d'entropia descriu com és d'irreversible un sistema termodinàmic.
Què és l'entropia estàndard?
L'entropia estàndard d'una composició química és la seva entropia sotmesa a 1 atm de pressió. Aquests valors s'expressen en una taula d'entropia que se sol indicar a una temperatura de 298 K.
Habitualment, en aquestes taules també s'expressen les entalpies de formació dels elements químics als seus estats estàndard establerts en zero. L'entalpia de formació és la quantitat d'energia necessària per formar aquestes composicions.
Fórmula de l'entropia a la física
En física, l'entropia és la magnitud termodinàmica que permet calcular la part de l'energia calorífica que no es pot utilitzar per produir feina si el procés és reversible. L'entropia física, en la seva forma clàssica, és definida per l'equació proposada per Rudolf Clausius:
![]()
o més simplement, si la temperatura es manté constant en el procés 1 → 2 ( procés isotèrmic ):
Així, si un cos calent a temperatura T1 perd una quantitat de calor Q1, la seva entropia disminueix en Q1/T1, Si cedeix aquesta calor a un cos fred a temperatura T2 (inferior a T1) l'entropia del cos fred augmenta més del que ha disminuït l'entropia del cos calent perquè
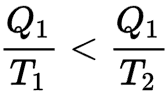
Una màquina reversible pot, doncs, transformar en feina una part d'aquesta energia calorífica.
Rendiment duna màquina tèrmica reversible
El rendiment que dóna la màquina reversible indica la relació màxima denergia útil que es pot convertir en treball. Aquesta relació es pot expressar mitjançant la fórmula següent:

Perquè tota l'energia calorífica es pogués transformar en feina caldria que, o bé el focus calent es trobés a una temperatura infinita, o bé que el focus fred estigués a zero kelvin; altrament, el rendiment termodinàmic de la màquina reversible és inferior a 1.
L'expressió de l'entropia és conseqüència lògica del segon principi de la termodinàmica i de la manera com es mesura la temperatura. La segona llei de la termodinàmica diu que, si no es consumeix feina, la calor flueix dels cossos calents als cossos freds.
Per què no es pot conèixer l'entropia absoluta?
Al món real no és possible determinar l'entropia absoluta perquè requeriria arribar a la temperatura de zero kelvin.
En física sempre es treballa en variacions d'entropia perquè per conèixer el valor absolut primer caldria poder arribar al 0 absolut. Per arribar al 0 absolut, el sistema necessitaria refredar-se a zero kelvin perquè les molècules ja no es moguin. A partir d´aquí, en augmentar la temperatura augmentaria l´entropia.
No obstant això, des d'un punt de vista físic, no és possible arribar a la temperatura de zero kelvin, segons el teorema de Walther Nernst presentat a la tercera llei de la termodinàmica.


