En geometria, els cossos geomètrics constitueixen una categoria essencial de formes tridimensionals que ocupen espai en tres dimensions: alt, ample i llarg. Aquests sòlids, definits per cares, arestes i vèrtexs, tenen un paper fonamental en la conceptualització i comprensió de les estructures tridimensionals.
La importància d'aquestes figures geomètriques tridimensionals rau en la seva capacitat per descriure objectes reals i abstractes a l'espai, i són crucials en camps com l'arquitectura, el disseny i l'enginyeria.
Un exemple clàssic és el cub, amb les sis cares quadrades i vèrtexs connectats, que representa un sòlid geomètric elemental. La diversitat de cossos geomètrics, des de piràmides fins a cilindres, permet modelar i comprendre la riquesa de formes que trobem al món tridimensional que ens envolta.
Què és un cos geomètric?
Un cos geomètric és una entitat tridimensional que ocupa espai en les dimensions d'alçada, amplada i profunditat. Diferenciant-se de les figures bidimensionals, aquests sòlids tridimensionals tenen cares, arestes i vèrtexs que en defineixen l'estructura. Els cossos geomètrics abasten diverses formes, des de prismes i piràmides fins a esferes i cilindres, cadascun amb propietats úniques.
Les cares planes, les vores definides i els vèrtexs connectats contribueixen a la caracterització d'aquests sòlids a l'espai tridimensional.
A més de la seva importància en geometria i matemàtiques, els cossos geomètrics s'utilitzen en aplicacions pràctiques en arquitectura, disseny i ciències, servint com a eines essencials per conceptualitzar i modelar objectes al món tridimensional.
Políedres: un cas particular
Els políedres són un cas particular de cossos geomètrics les cares dels quals són tots polígons. Entre ells, podem distingir políedres regulars i políedres irregulars.
A la geometria tridimensional, un poliedre és l'equivalent a un polígon qualsevol a la geometria de dues dimensions.
Els políedres regulars estan formats per polígons regulars. Aquests cossos geomètrics es poden classificar segons el nombre de cares.
Els políedres regulars són els més simètrics. Hi ha un total de nou políedres regulars: cinc políedres convexos i quatre políedres d'estrelles.
Un poliedre convex és un poliedre que materialitza un sòlid convex, és a dir, per a cada parell de punts al sòlid, el segment lineal que els uneix està completament contingut en el sòlid.
Els cinc exemples convexos es coneixen des de l'antiguitat i s'anomenen políedres platònics. Aquests són la piràmide triangular o el tetraedre, el cub, l'octaedre, el dodecaedre i l'icosàedre.
Tronc de piràmide
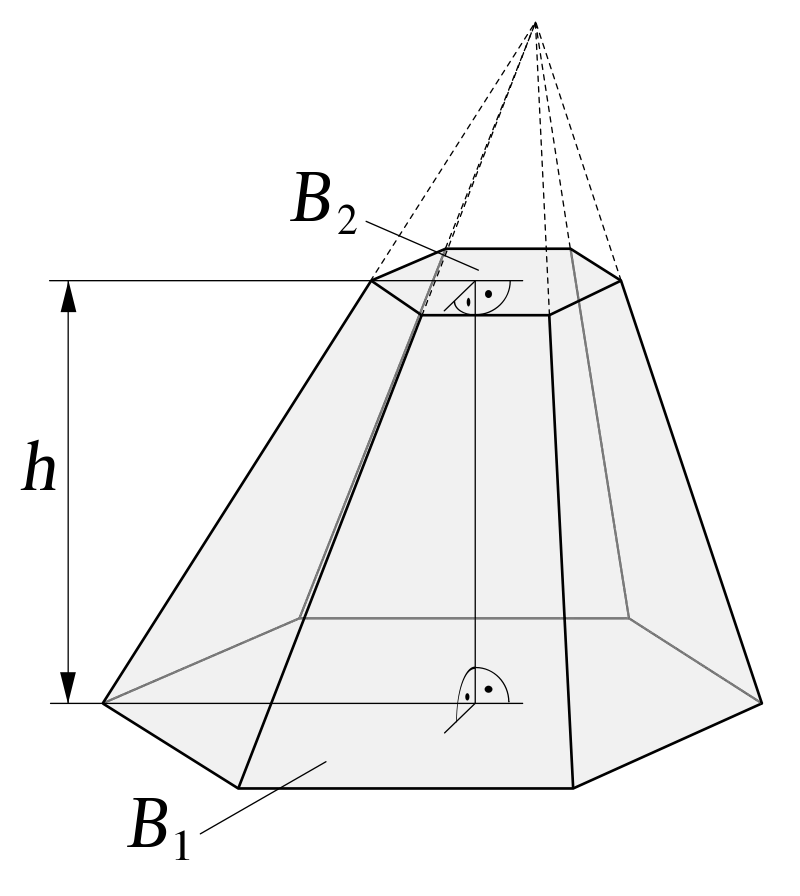El tronc de piràmide és un tipus de poliedre compost per dues bases paral·leles amb el mateix nombre d'arestes. D'altra banda, està composat per cares laterals en forma de trapezi. El nombre de cares és el mateix que el de les arestes de les bases.
Aquest poliedre s'obté en seccionar una piràmide amb un pla intermedi i paral·lel a la base. Dels dos trossos resultants, la part inferior és un tronc de piràmide i la part superior continua sent una piràmide.
Prismes
Un prisma és un poliedre, dues de les cares són iguals i que es troben en plans paral·lels. Les cares restants del prisma són paral·lelograms que tenen costats comuns amb aquests polígons. Aquests paral·lelograms es diuen cares laterals del prisma, i els dos polígons restants es diuen bases.
El polígon que es troba a la base determina el nom del prisma, per exemple: si les bases són triangles és un prisma triangular.
Segons la base, el prisma es pot anomenar com:
- Prisma triangular: cada base té forma de triangle.
- Prisma quadrangular: té cadascuna de les bases en forma de quadrilàter.
- Prisma pentagonal: té cadascuna de les bases en forma de pentàgon.
- Prisma hexagonal: cadascuna de les bases té forma d'hexàgon.
- Prisma octogonal: té cadascuna de les bases amb forma d'octàgon.
Cossos rodons
Definim els cossos rodons com els cossos geomètrics que almenys tenen una cara corba. Aquest tipus de cos també es coneixen com a cossos de revolució perquè es poden obtenir fent girar una figura geomètrica al voltant d'un eix.
Alguns exemples de cossos rodons són:
- L'esfera és la figura generada en girar un cercle mitjançant un eix que passa pel centre. En aquest cas té una única superfície corba i no té arestes. A més a més, tots els punts de la superfície són equidistants al centre de l'esfera.
- El con es genera en revolucionar un triangle rectangle al voltant d'un dels seus catets. Aquesta figura té una única cara plana formada per un cercle.
- El cilindre es forma girant un rectangle al voltant d'un costat.
Exemples quotidians
- Pilota de futbol Exhibint la perfecció d'una esfera, la pilota de futbol il·lustra la presència comuna d'aquesta forma geomètrica en objectes quotidians.
- Planetes del Sistema Solar Els cossos celestes del Sistema Solar adopten formes esfèriques, destacant la prevalença de l'esfera en la configuració de l'univers.
- Caixa de cartró Amb la seva estructura que segueix la forma d'un prisma rectangular, conegut com a ortoedre, les caixes de cartró són exemples tangibles de figures geomètriques en envasos comuns.
- Piràmides d'Egipte Representant la majestuositat arquitectònica, les piràmides són exemples de piràmides quadrangulars que han resistit el pas del temps.
Aquests exemples il·lustren com la geometria està intrínsecament present al nostre entorn, des d'objectes quotidians fins a monuments històrics.